Basic sorting algoritm
이번 Posting에서는 기본적인 sorting들에 대하여 정리를 할 것이다.
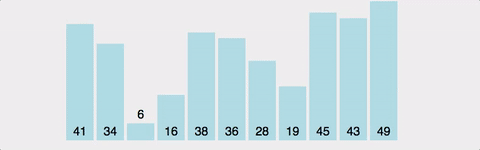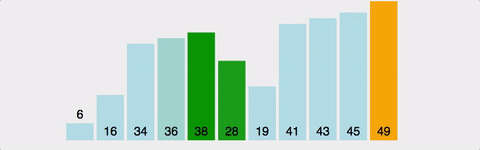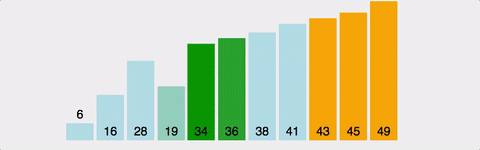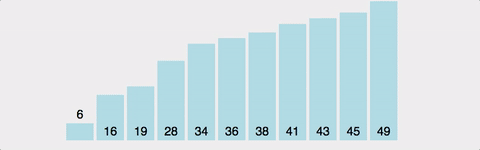
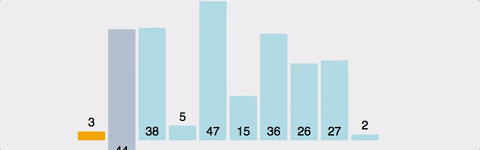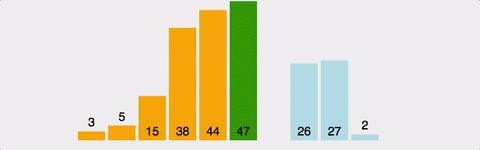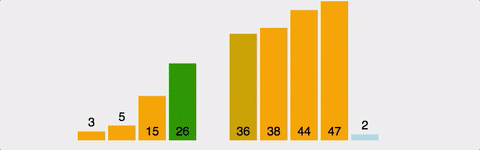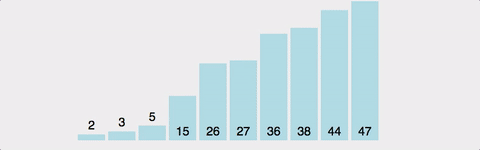
여담이지만 버블 정렬이 왜 버블 정렬인지 생각해본적이 있나?
위 이미지를 왼쪽으로 90도 회전시키면 위로 올라가는 모양이 된다 그래서 거품이 올라가는 형상같다고하여 버블 소트라고 이름이 붙은 것이다.
구현이 간단하다. 시간 복잡도는 O(N^2)으로 좋은 퍼포먼스를 가진 것은 아니다.
선택 정렬 코드
힙 정렬 코드
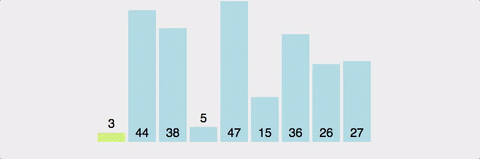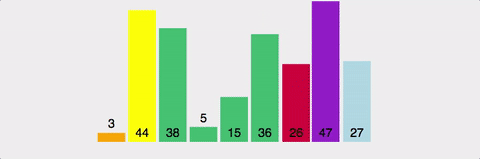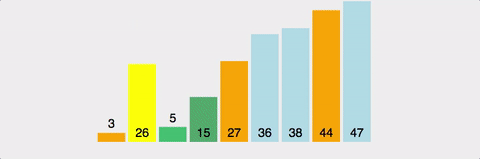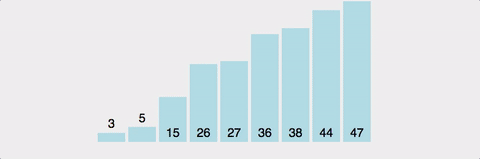
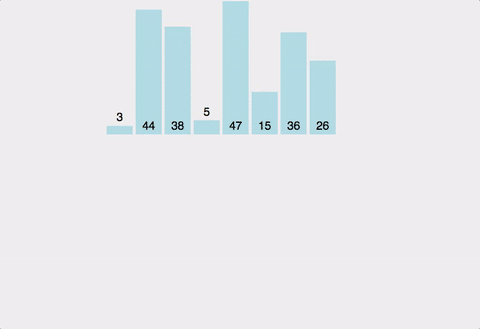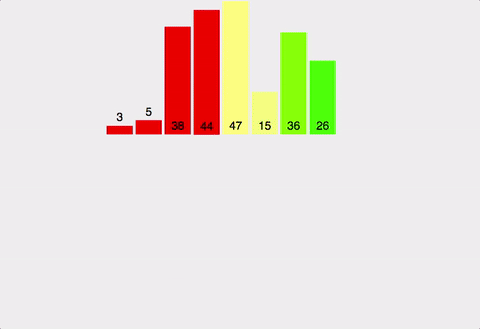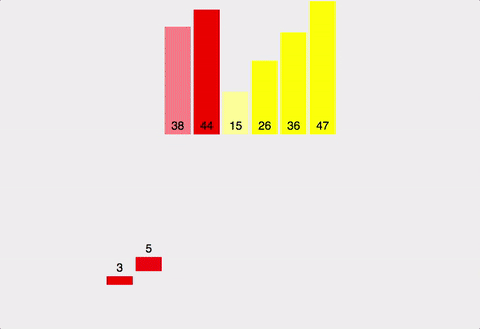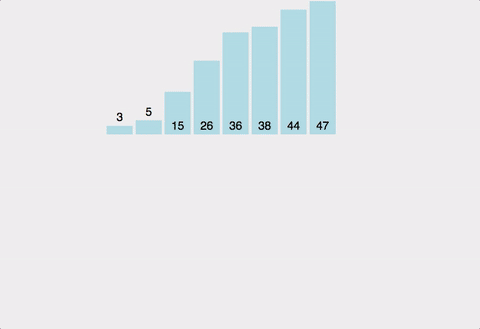
이상으로 Posting을 마친다. (위의 그림의 출처: https://cdn-images-1.medium.com )
- Bubble sort(버블 정렬)
- Insertion sort(삽입 정렬)
- Selection sort(선택 정렬)
- Heap sort(힙 정렬)
- Quick sort(퀵 정렬)
- merge sort(병합 정렬)
1. Bubble sort(버블 정렬)
거품 정렬은 정렬을 처음 배울 때 나오는 녀석이다. 가장 직관적이고 이해하기 쉽기 때문에 처음에 배우는 것이라고 생각한다. 이 녀석의 시간 복잡도는 O(N^2) 즉 for문 2개로 정렬을 할 수가 있다. 쉽지만 퍼포먼스가 떨어지기 때문에 잘 사용하지 않는다.
버블 정렬 코드
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | public class BubbleSort { static int[] data = {14, 6, 45, 43, 41, 28, 38, 36, 49, 16, 34}; public static void main(String[] args) { bubbleSort(); for (int i = 0; i < data.length; i++) { System.out.print(data[i]); if (i < data.length - 1) System.out.print(" "); } } public static void bubbleSort() { for (int i = 0; i < data.length; i++) { for (int j = 1; j < data.length - i; j++) { if (data[j] < data[j - 1]) { int tmp = data[j - 1]; data[j - 1] = data[j]; data[j] = tmp; } } } } } |

여담이지만 버블 정렬이 왜 버블 정렬인지 생각해본적이 있나?
위 이미지를 왼쪽으로 90도 회전시키면 위로 올라가는 모양이 된다 그래서 거품이 올라가는 형상같다고하여 버블 소트라고 이름이 붙은 것이다.
2. Insertion sort(삽입 정렬)
삽입 정렬은 간단하게 말해서 앞에서부터 정렬을 하는데 현재 index의 크기를 판단해서 적절한 위치에 삽입을 하는 로직이다. 삽입 정렬은 이미 정렬이 되어있다면 O(N)의 복잡도를 갖는다. 왜냐하면 배열을 보면서 바꿔줄 녀석이 없으면 삽입하는 loop를 돌지 않아도 되기 때문이다. 하지만 보통의 경우 Bic-O O(N^2)의 복잡도를 갖는다.
삽입 정렬 코드
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 | public class InsertionSort { static int[] data = {14, 6, 45, 43, 41, 28, 38, 36, 49, 16, 34}; public static void main(String[] args) { insertionSort(); for (int i = 0; i < data.length; i++) { System.out.print(data[i]); if (i < data.length - 1) System.out.print(" "); } } public static void insertionSort() { for (int i = 1; i < data.length; i++) { int tmp = data[i], here = i - 1; for (int j = i - 1; j > -1; j--) { if (data[j] > tmp) { data[j + 1] = data[j]; }else { here = j + 1;break; } } data[here] = tmp; } } } |

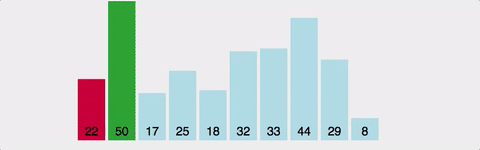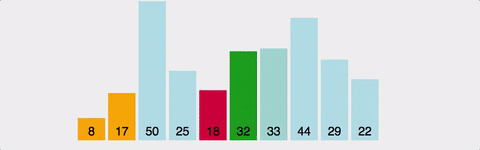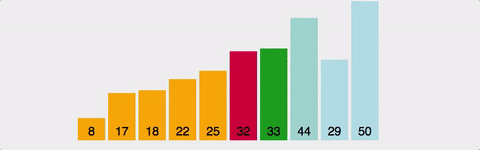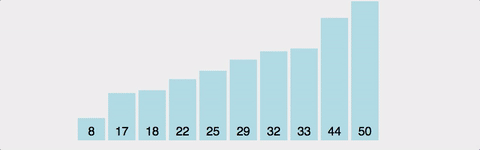
3. selection sort(선택 정렬)
선택 정렬도 버블 정렬과 마찬가지로 가장 이해하기 쉬운 로직으로 구현된 정렬 방식이다.구현이 간단하다. 시간 복잡도는 O(N^2)으로 좋은 퍼포먼스를 가진 것은 아니다.
선택 정렬 코드
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | public class SelectionSort { static int[] data = {14, 6, 45, 43, 41, 28, 38, 36, 49, 16, 34}; public static void main(String[] args) { selectionSort(); for (int i = 0; i < data.length; i++) { System.out.print(data[i]); if (i < data.length - 1) System.out.print(" "); } } public static void selectionSort() { for (int i = 0; i < data.length - 1; i++) { for (int j = i + 1; j < data.length; j++) { if (data[i] > data[j]) { int tmp = data[i]; data[i] = data[j]; data[j] = tmp; } } } } } |

4. Heap sort(힙 정렬)
힙 정렬은 자료구조인 heap을 이용하여 정렬을 하는 것으로 자세한 내용은 data structure 탭에 있다. 다음 코드는 heap으로 구현된 우선순위 큐를 활용한 방법이다.힙 정렬 코드
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | import java.util.PriorityQueue; import java.util.Queue; public class HeapSort { static int[] data = {14, 6, 45, 43, 41, 28, 38, 36, 49, 16, 34}; static Queue priorityQueue = new PriorityQueue(); public static void main(String[] args) { for (int i = 0; i < data.length; i++) { priorityQueue.add(data[i]); } heapSort(); } public static void heapSort() { while (!priorityQueue.isEmpty()) System.out.print(priorityQueue.poll() + " "); } } |
5. Quick sort(퀵 정렬)
퀵 정렬은 흔하게 사용하는 정렬 알고리즘으로 어떤 pivot 값을 정하고 왼쪽과 오른쪽에 각각 작은 것과 큰것을 배치시킨다. 이러한 로직을 왼쪽 오른쪽으로 분할하여 정렬한다.
최악의 경우 O(N^2)의 복잡도를 갖지만 일반적으로는 O(NlogN)의 복잡도를 갖는다.
최악의 경우 O(N^2)의 복잡도를 갖지만 일반적으로는 O(NlogN)의 복잡도를 갖는다.
위에서 언급한 최악의 경우는 정렬이 되어있는 배열을 정렬하려고할 때 발생한다. 그 이유는 첫번 째 인덱스의 값을 pivot으로 결정한 경우, 분할되지 못하고 한번의 라운드에 n번의 비교를 해야하기 때문이다.
퀵 정렬 코드
퀵 정렬 코드
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 | public class QuickSort { static int[] data = {14, 6, 45, 43, 41, 28, 38, 36, 49, 16, 34}; public static void main(String[] args) { quickSort(data, 0, data.length - 1); for (int i = 0; i < data.length; i++) { System.out.print(data[i]); if (i < data.length - 1) System.out.print(" "); } } public static void quickSort(int[] arr, int l, int r) { int left = l, right = r; int pivot = arr[(l + r) / 2]; do{ while (arr[left] < pivot) left++; // find index that higher than pivot while (arr[right] > pivot) right--;// find index that lower than pivot if (left <= right) { int tmp = arr[left]; arr[left] = arr[right]; arr[right] = tmp; left++;right--; } }while (left <= right); if (l < right) quickSort(arr, l, right); if (r > left) quickSort(arr, left, r); } } |

6. merge sort(병합 정렬)
병합 정렬은 정렬할 배열을 반으로 쪼개면서 좌우 배열을 계속해서 분할한 후 각 배열 내에서 정렬을 한 후 다시 합치는 과정을 통해 정렬하는 알고리즘이다. 시간 복잡도는 O(NlogN)을 보장한다. 하지만 단점은 배열을 2개 쓰기 때문에 공간 복잡도가 올라긴다.
병합 정렬 코드
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 | public class MergeSort { static int[] sortedArray = new int[11]; public static void main(String[] args) { int[] data = {14, 6, 45, 43, 41, 28, 38, 36, 49, 16, 34}; mergeSort(data, 0, data.length - 1); for (int i = 0; i < sortedArray.length; i++) { System.out.print(sortedArray[i]); if (i < sortedArray.length - 1) System.out.print(" "); } } public static void mergeSort(int[] arr, int m, int n) { int mid; if (m < n) { mid = (m + n) >> 1; mergeSort(arr, m, mid); mergeSort(arr, mid + 1, n); merge(arr, m, mid, n); } } public static void merge(int[] arr, int m, int mid, int n) { int i = m, j = mid + 1, k = m; while (i <= mid && j <= n) { sortedArray[k] = (arr[i] <= arr[j]) ? arr[i++] : arr[j++]; k++; } int start = (i > mid) ? j : i, end = (i > mid) ? n : mid; for (int t = start; t <= end; t++, k++) { sortedArray[k] = arr[t]; } for (int t = m; t <= n; t++) { arr[t] = sortedArray[t]; } } } |

이상으로 Posting을 마친다. (위의 그림의 출처: https://cdn-images-1.medium.com )